基本块和 Traces

约 2522 个字 预计阅读时间 8 分钟

规范形式

语义分析阶段生成的树必须翻译成汇编语言或机器语言。Tree 语言的运算符经过精心选择，以匹配大多数机器的功能，但是

• Tree 语言的某些方面与机器语言并不完全对应
• Tree 语言的某些方面会干扰编译时优化分析

例如

• CJUMP 会在两个分支之间选择一个跳转
  • 真正的汇编指令里有 conditional jump，在条件成立会跳转，条件不成立的情况下就执行自己的后一条指令
  • 而在 IR tree 里无论成立还是不成立，都需要跳转
• 表达式内的 ESEQ 结点不方便
  • 评估子树的不同顺序会产生不同的结果（因为执行 s 时的副作用）
  • 但是能够以任意顺序计算表达式的子表达式是很有用的
• 表达式中的 CALL 结点也依赖于顺序（有副作用）
  • 当尝试将参数放入一组固定的形式参数寄存器时
  • 例如，CALL(f, [e1, CALL(g, [e2, ...])])
• 中间代码具有通用树形形式
  • 易于从 AST 生成
  • 但很难直接转换为汇编（汇编代码是一系列语句）

因此，需要将 IR 转换为规范形式以消除以上的问题

这就引入了规范形式的概念：

• 所有 SEQ 结点都沿着右链
• 所有语句都带到树的顶层
• 可以直接生成程序集

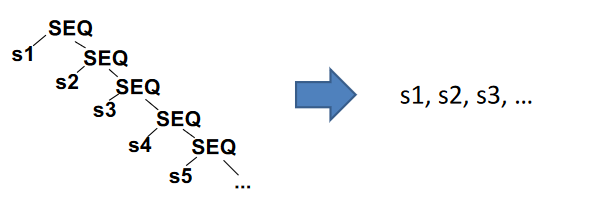
一个函数只是一个包含所有内容的大 SEQ 语句，从而可以更加方便地转换为汇编代码

为了实现转换为规范形式的目标，可以分三个阶段改造 IR 树：

• 将一棵树重写为不带 SEQ 或 ESEQ 结点的一系列规范树（canonical trees）
• 该列表被分组为一组基本块（basic blocks），其中不包含内部跳转或标签
• 基本块被排序为一组 traces，其中每个 CJUMP 后面紧跟着其错误分支的标签

规范树（线性化）的过程

规范树（Canonical Trees）具有如下的性质：

• 无 SEQ 或 ESEQ
• 每个 CALL 的父级是 EXP(...) 或 MOVE(TEMP t, ...)

因此：

• 每棵规范树只包含一个语句结点，即根结点，其他结点均为表达结点
• CALL 结点的父结点必须是一颗规范树的根结点，且必须是 EXP(...) 或 MOVE(TEMP t, ...)
• 一棵规范树中只能有一个 CALL 结点，因为 EXP(...) 和 MOVE(TEMP t, ...) 只能包含一个 CALL

消除 ESEQ（ESEQ 的线性化规则）

如何消除 ESEQ 结点

将它们在树中提升得越来越高，直到它们成为 SEQ 结点

具体的规则包括：

原始	转换后
ESEQ(s1, ESEQ(s2, e))	ESEQ(SEQ(s1,s2), e)
BINOP(op, ESEQ(S, e1), e2)	ESEQ(s, BINOP(op, e1, e2))
MEM(ESEQ(s,e1))	ESEQ(s, MEM(e1))
JUMP(ESEQ(s, e1))	SEQ(s, JUMP(e1))
CJUMP(op, ESEQ(s, e1), e2, l1, l2)	SEQ(s, CJUMP(op, e1, e2, l1, l2))

接着考虑副作用对线性化规则的影响，考虑 BINOP(op, e1, ESEQ(s, e2))，因为 s 可能有影响 e1 值的副作用，所以不能直接互换 s 和 e1 的顺序，可以使用临时存储 e1 的值

交换性

交换性（Commutativity）：如果 s 不影响 e 的值，则语句 s 和表达式 e 可以交换

若不可交换，则可能需要引入临时变量来保存 e 的值，从而得到规范树

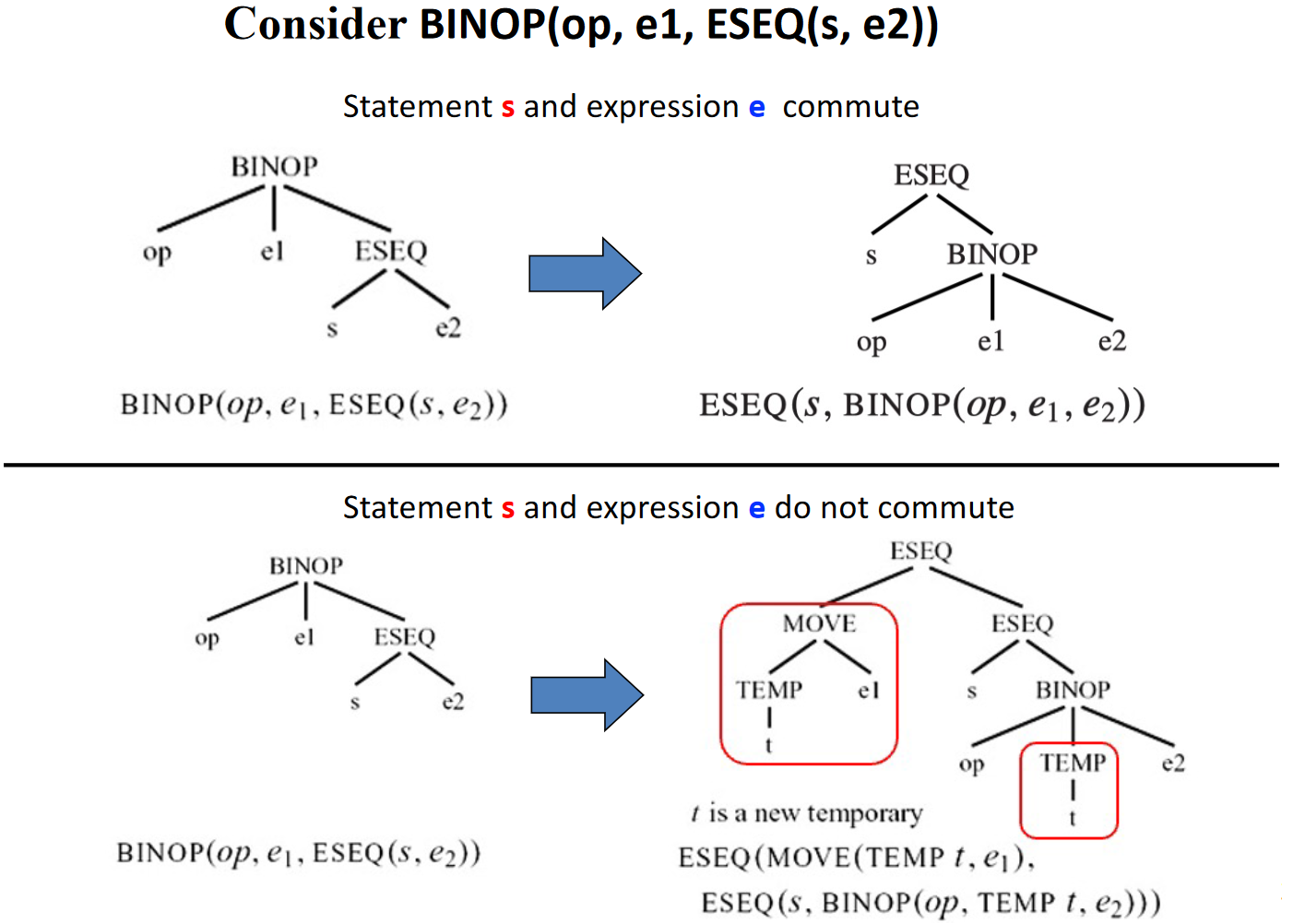
由此，我们可以得到在不同交换性下的转换规则：

• 如果 s e1 是可交换的

  原始	转换后
  BINOP(op, e1, ESEQ(s, e2))	ESEQ(s, BINOP(op, e1, e2))
  CJUMP(op, e1, ESEQ(s, e2), l1, l2)	SEQ(s, CJUMP(op, e1, e2, l1, l2))

• 如果 s e1 是不可交换的

  原始	转换后
  BINOP(op, e1, ESEQ(s, e2))	ESEQ(MOVE(TEMP t, e1), ESEQ(s, BINOP(op, TEMP t, e2)))
  CJUMP(op, e1, ESEQ(s, e2), l1, l2)	SEQ(MOVE(TEMP t, e1), SEQ(s, CJUMP(op, TEMP t, e2, l1, l2)))

但是我们很难静态地确定语句 s 与表达式 e 是否可以交换，因此需要做一个保守的近似（conservative approximation）。这种近似可以如下：

• 常量可与任何语句交换
• 空语句可与任何表达式交换
• 假设任何其他情况都不具备交换性

一些扩展内容

BINOP 和 MOVE 的规则依赖于交换较低位置的语句 s 和表达式 e 的顺序，当 s 无法改变 e 中使用的值时，可以安全地完成此操作

语句 s 和表达式 e 不能互换的两个条件

• 该语句可以更改表达式使用的临时变量的值
• 该语句可以更改表达式使用的内存位置的值

为了检查这两点

• 临时变量：很容易确定语句是否更新表达式使用的临时变量，因为临时变量具有唯一的名称
• 内存：这要困难得多，因为两个内存位置可能是别名（aliases）关系

因此更精确（但仍然保守）的近似可以使用一些别名分析技术

将 CALL 移至顶层

在现代处理器中，函数调用的返回值一般保存到专用的寄存器中，那么考虑 BINOP(PLUS, CALL(...), CALL(...))，第二次调用的返回值会覆盖第一次调用的返回值

因此，我们可以立即将每个返回值分配到一个新的临时寄存器中，并把 CALL 移至顶层

CALL(fun, args) -> ESEQ(MOVE(TEMP t, CALL(fun, args)), TEMP t)

消除 SEQ

应用上述规则后，我们可以得到 SEQ(SEQ(SEQ(..., sx), sy), sz) 的形式，只需要重复利用如下规则

SEQ(SEQ(a, b), c) = SEQ(a, seq(b, c))

即可获得如下形式的表达式

SEQ(s1, SEQ(s2, ..., SEQ(sn-1, sn)...))

进而将其看作一个简单的语句列表

s1, s2, ..., sn, ...

其中每个 si 均不包含 SEQ/ESEQ 结点

处理条件分支

CJUMP 的问题：在大多数机器上没有双向分支的对应项

目标：重新排列树，使得 CJUMP(cond, l_t, l_f) 被 LABEL(l_f) 紧跟着

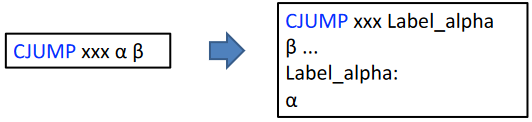
解决方案：

• 将规范树列表形成基本块（basic block）
• 将基本块排序为 traces

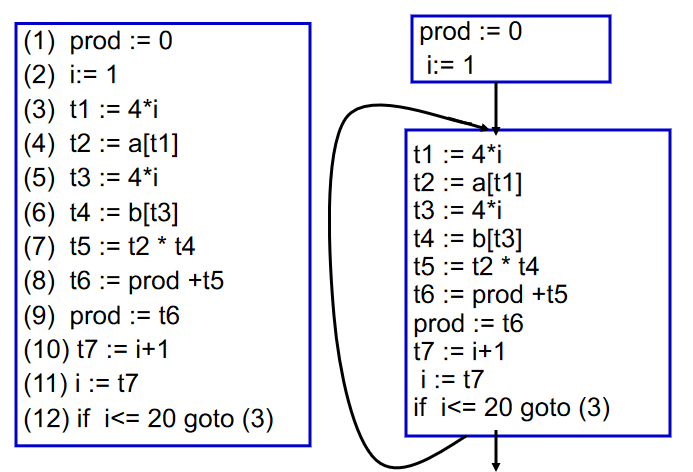
Basic Blocks

基本块（basic block）是始终在开头输入并在结尾退出的语句序列，即：

• 第一个语句是一个 LABEL
• 最后一条语句是 JUMP 或 CJUMP
• 该块中没有其他 LABEL、JUMP 或 CJUMP

构建算法为：

• 从头到尾扫描
• 当找到标签（包括跳转的目的地址）时，结束前一个块并开始一个新块并
• 每当找到 CJUMP/JUMP 时，当前块就会结束并开始下一个块
• 如果留下了一个没有 CJUMP/JUMP 结尾的块，则附加一个到下一个块的跳转
• 如果一个块在开始时没有标签，添加一个标签

Basic Blocks

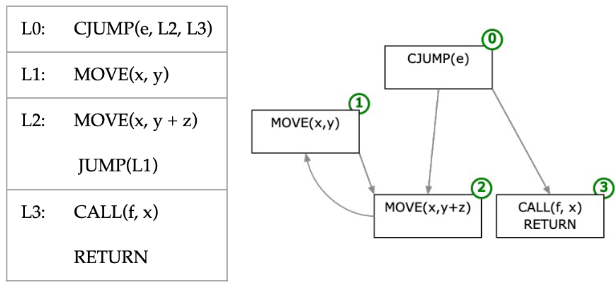
此外，引入控制流图（Control Flow Graph，CFG）：结点是基本块，边是它们之间的跳转关系。在某些情况下，CFG 的结点是一条语句（如活跃变量分析和寄存器分配部分）

Control Flow Graph

Traces

基本块可以按任意顺序排列，执行程序的结果将是相同的。基于这个属性，我们可以优化跳转的性质和次数：

• 选择块的顺序，使得每个 CJUMP 都被它的错误分支跟着
• 安排许多无条件 JUMP 后紧跟着其目标标签
  • 这样可以允许删除无条件跳转，使得编译后的程序运行得更快一些
• *其他方面：可能还可以优化指令缓存等

Basic Block Reordering

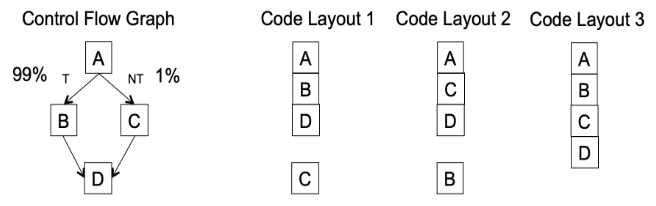
99% 和 1% 代表执行频率。可以看到，Code Layout 1 减少了指令预取的中断，提高了 I-cache 的命中率

找到基本块的良好排序的常用技术是构造 trace

Trace: 执行过程中可以连续执行的语句序列（或者说一系列基本块）

A covering set of traces: 每条 trace 都是无循环的，且每个块必须恰好位于一个 trace 中

生成 covering set of traces 的基本算法是对 CFG 的深度优先遍历：

• 从某个 basic block 开始，往后继结点遍历，标记每个被访问的 basic block 并将其附加到当前 trace 中
• 当到达某个 basic block，其后继结点均已标记，这个 trace 就算完了
• 选择一个未标记的 basic block 作为下一个 trace 的起点，不断迭代，直到所有的 basic blocks 都被标记

\begin{algorithm}
\caption{Generating a Covering Set of Traces}
\begin{algorithmic}
\State Put all the blocks of the program into a list $Q$
\While{$Q$ is not empty}
    \State start a new (empty) trace, call it $T$
    \State remove the head element $b$ from $Q$
    \While{$b$ is not marked}
        \State mark $b$; append $b$ to the end of the current trace $T$;
        \State examine the successors of $b$
        \If{there is any unmarked successor $c$}
            \State $b \gets c$
        \EndIf
    \EndWhile
    \State end the current trace $T$
\EndWhile
\end{algorithmic}
\end{algorithm}

Generating a Covering Set of Traces

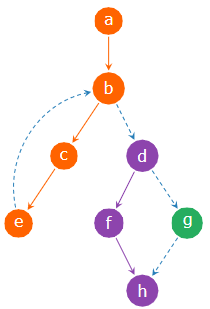
Covering set of traces:

• {a, b, c, d}
• {d, f, h}
• {g}

考虑跳转

我们更喜欢 CJUMP 后跟其错误标签，因为这可以转换为机器代码中的条件跳转，因此：

• 对于任何 CJUMP 后跟其真实标签分支的情况
  • 交换真假标签并反转条件
• 对于任何 CJUMP 后跟其错误标签分支的情况
  • 这是我们想要的情况，不需要做任何事情
• 对于任何后面没有标签的 CJUMP(cond, a, b, lt, lf)
  • 替换为

    CJUMP(cond, a, b, lt, lfʹ)
    LABEL lfʹ
    JUMP(NAME lf )
    

对于无条件跳转 JUMP，若一个 JUMP 被其目标标签紧跟着，则可以删除这个 JUMP

最优 Traces

“最优”需要标准，例如，任何频繁执行的指令序列（例如循环体）应该具有自己的 trace：

• 这有助于减少无条件跳转的数量
• 这有助于其他类型的优化
  • 寄存器分配
  • 指令调度
  • ...

Optimal Traces

(a): While循环的每个迭代有一个 CJUMP 和一个 JUMP
(b): 使用了不同 traces, 但每个迭代仍有一个 CJUMP 和一个 JUMP
(c): 每个迭代都没有 JUMP

---

最后更新: 2025年3月26日 17:22:55
创建日期: 2024年6月22日 00:07:07